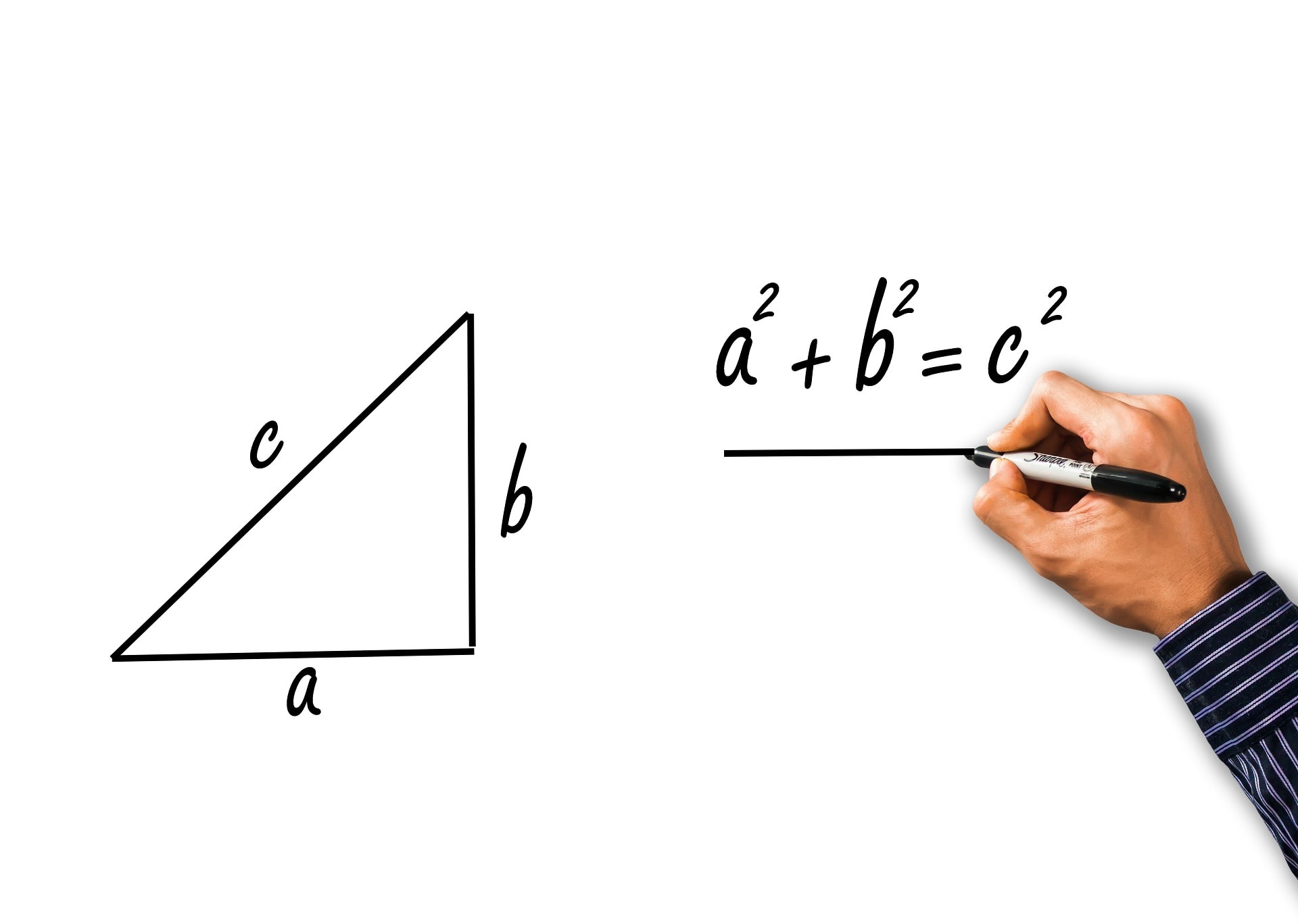Mówiąc krótko, a2 + b2 = c2. Taka zależność jest kluczowa dla trygonometrii, choć zdaniem niektórych nie powinno dać się udowodnić samego twierdzenia z wykorzystaniem zasad rządzących tą dziedziną. Z błędu wyprowadziły ich dwie licealistki z Nowego Orleanu.
Czytaj też: Kapelusz “Einsteina” nowym łupem matematyków. To nieznany wcześniej kształt
Działający w VI i V wieku p.n.e. grecki matematyk zaproponował twierdzenie, którego nie udało się obalić nawet najtęższym umysłom tego świata, którym przyszło żyć na Ziemi po nim. Jeśli natomiast chodzi o próby potwierdzenia założeń Pitagorasa, to udało się tego dokonać wielokrotnie, lecz nie w oparciu o trygonometrię.
Na przykład Elisha Loomis w swojej książce na ten temat stwierdził że brakuje brakuje dowodów trygonometrycznych umacniających twierdzenie Pitagorasa, ponieważ wszystkie podstawowe wzory trygonometrii są oparte właśnie na prawdziwości jego założeń. Od wydania dzieł Loomisa minęło już wiele lat, a uczennice liceum w Nowym Orleanie: Calcea Johnson i Ne’Kiya Jackson, udowodniły, że matematyk się mylił.
Licealistki, aby udowodnić twierdzenie Pitagorasa, wykorzystały założenia z dziedziny trygonometrii
Jak twierdzą przedstawicielki St. Mary’s Academy, prawo sinusów może być wykorzystane do udowodnienia twierdzenia Pitagorasa. Wykorzystując wzór sinusów i unikając tożsamości trygonometrycznej twierdzenia Pitagorasa, licealistki wykazały, że założenia starożytnego matematyka były zgodne z prawdą. Głos w sprawie zabrało nawet Amerykańskie Towarzystwo Matematyczne, które zachęca młode entuzjastki matematyki do przesłania swoich prac do recenzowanego czasopisma.
Czytaj też: Model matematyczny Alana Turinga w końcu potwierdzony. Wystarczyły do tego nasiona chia
Oczywiście nie jest to pierwszy taki przypadek w historii: wcześniej matematycy również potwierdzili założenia Pitagorasa korzystając z sinusów i cosinusów, bez polegania na sin²α + cos²α = 1. Nie ma co jednak umniejszać geniuszu licealistek. Dość powiedzieć, że Albert Einstein udowodnił twierdzenie Pitagorasa w wieku 12 lat. Czyżby teraz nadeszła pora na Einsteina w spódnicy?