Jak wyjaśniają autorzy badań, którzy zaprezentowali swoje dotychczasowe ustalenia w formie preprintu, przyszła pora na pewne zmiany. Te nie są może przełomowe z punktu widzenia matematyki, lecz robią wrażenie, jeśli mamy na uwadze długoletni przestój w tej sprawie.
Czytaj też: Komputer kwantowy zadebiutował w chemii. Naukowcy są podekscytowani możliwościami
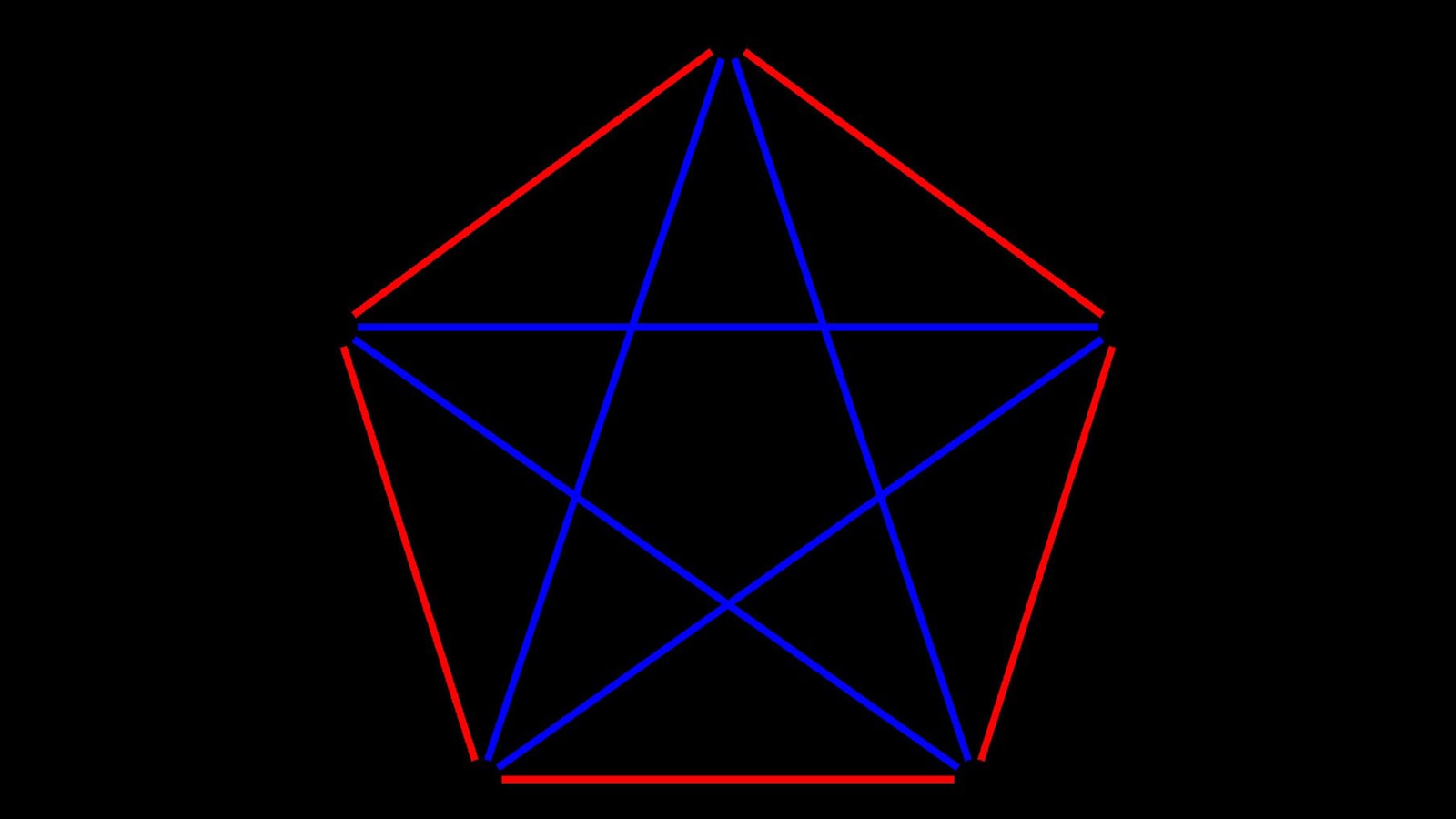
Na czym w ogóle polega twierdzenie Ramseya? Najkrócej rzecz ujmując, odnosi się ono do teorii grafów i sięga czasów Franka Ramseya, angielskiego matematyka zajmującego się między innymi zagadnieniami z dziedziny kombinatoryki. Ta obejmuje badania nad liczbami naturalnymi oraz sposobami ich układania w grupy czy też innymi problemami. Kwestie związane z kombinatoryką są stosunkowo rozległe, dlatego mogą dotyczyć nawet algebry, geometrii, biologii czy programowania.
Jeśli zaś chodzi o dokładne wyjaśnienie, czym jest liczba Ramseya to można ją opisać mianem minimalnej wielkości grupy potrzebnej do zapewnienia, że pewna liczba węzłów w tej grupie jest ze sobą połączona. Czasami naukowcy wyjaśniają tę kwestię wykorzystując analogię do… przyjęcia. Ile osób należy zaprosić, aby mieć pewność, że będzie to grupa trzech osób, które się znają bądź trzech osób, które są sobie zupełnie obce?
Twierdzenie Ramseya sięga ubiegłego stulecia. W 1935 roku węgierski matematyk Paul Erdős zaproponował górną granicę tej liczby
Liczba Ramseya dla 3 to 6. A żeby mieć pewność, że dana impreza ma grupę czterech przyjaciół lub czterech nieznajomych, należy powiększyć listę gości do 18 osób. W przypadku 5 liczba Ramseya będzie wynosić od 43 do 48. Im wyższe liczby, tym trudniej pozyskać rozwiązanie, ponieważ więcej węzłów w sieci oznacza więcej możliwych połączeń i możliwych struktur dla powstałego grafu.
W 1935 roku węgierski matematyk Paul Erdős udowodnił, że górna granica liczby Ramseya wynosi cztery do wykładnika pożądanej wielkości. Z kolei autorzy nowych badań sądzą, iż górna granica jest o 0,007 niższa i wynosi 3,993 do tej samej potęgi. Innymi słowy, zamiast 4 do potęgi N, maksymalna liczba Ramseya dla danej sieci wynosi 3,993 do potęgi N. Na przykład 4 do potęgi szóstej to 4096, ale 3,993 do potęgi szóstej to 4053,18. Różnica nie jest więc gigantyczna, ale bez wątpienia zauważalna.
Czytaj też: Model matematyczny Alana Turinga w końcu potwierdzony. Wystarczyły do tego nasiona chia
I choć wszystko to brzmi nieco skomplikowanie, to warto jednocześnie zauważyć, że liczby Ramseya… nie mają konkretnego zastosowania w świecie rzeczywistym. Z drugiej strony, w latach 80. ubiegłego wieku matematycy badali teorię Ramseya z wykorzystaniem koncepcji zwanej quasi-losowością. Ta obecnie jest bardzo ważna dla dziedziny informatyki. Twierdzenia Ramseya w jakimś stopniu spopularyzowało tę koncepcję.